Флексагон – увлекательная математическая игрушка

Если бы не одна незначительная деталь – разница в форматах бумаги – возможно, мир никогда бы не узнал о такой удивительной поделке, как флексагон. В конце 30-х годов прошлого века английский студент Артур Стоун поступил в Принстонский университет, где начал изучать математику. Именно тогда он столкнулся с тем, что американский формат бумагиLetter немного короче привычного международного А4. Подрезав свой блокнот под новые стандарты, он машинально покрутил в руках обрезки и неожиданно получил шестиугольную фигурку.

Сложенный шестиугольник обладал интересными возможностями – когда одни грани подгибались внутрь, наружу выходили те, что раньше были спрятаны. Артур Стоун поделился открытием с друзьями, совместными усилиями они создали более сложные варианты бумажных шестиугольников. Они получили название флексагон, от английского flex – сгибать. Приставка перед названием означала количество углов в фигуре, например, шестиугольник назвали гескафлексагоном. Еще одна приставка указывала на количество поверхностей, спрятанных в поделке.

Будущие гении науки собирались в студенческой столовой, обмениваясь идеями и усовершенствуя изобретение. Они называли себя «Флексагонным комитетом» и всерьез изучали математические основы своего открытия. Уже к началу следующего десятилетия Комитет разработал глубокую теорию основ «флексологии», использование которой позволяло построить флексагон из бумаги с любым количеством граней и слоев.

Разновидности флексагона

Изначально флексагон состоял только из равносторонних треугольников, сложенных под углом 60 градусов. Со временем, члены «Флексагонного комитета» расширили его возможности, они научились складывать флексагоны из равнобедренных треугольников, квадратов, пятиугольников и других фигур. Чаще всего встречаются квадратные и шестиугольные флексагоны:

Как указывалось выше, название флексагона можно разложить на формулу: числовая приставка, означающая количество поверхностей+приставка, означающая количество углов+флексагон.

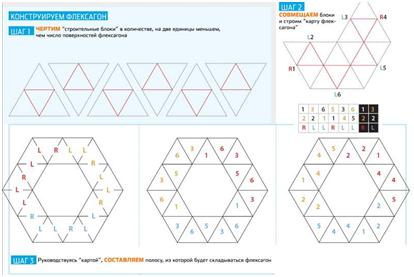В зависимости от числа поверхностей и углов различают следующие виды флексагонов.

Гексафлексагоны. Как понятно из названия, эта поделка обладает формой правильного шестиугольника. Все слои-поверхности флексагона составлены из 6 равных треугольников. Этот вид флексагонов обладает огромным количеством подвидов, различающихся по количеству вложенных поверхностей. Их число ограничивается только тем, что бумага имеет свою толщину. Известны гексафлексагоны даже с 42 поверхностями. Самый первый, наиболее простой вариант, который подойдет для начинающих, – три гексафлексагон. У него всего три доступных поверхности. Складывают три гексафлексагон из полосы бумаги, разделенной на десять равносторонних треугольных секторов. Один из самых популярных вариантов гексафлексагона – гексагексафлексагон, шестиугольник с шестью поверхностями. Именно с него, чаще всего, начинается знакомство с флексагонами, так как техникам его складывания посвящено множество подробных мастер-классов.

Тетрафлексагон. Составленный в форме квадрата флексагон может иметь от трех поверхностей. Гекса- и декатетрафлексагоны собирают из крестообразной основы-развертки или квадратной рамки (в этом случае количество поверхностей можно рассчитать по формуле 4n+2). Используя заготовку в форме зигзага можно сложить тетратетрафлексагон и квадратные флексагоны, количество поверхностей которых кратно четырем.

Кольцевые флексагоны. Особый вид флексагонов, их поверхность составлена из кольца многоугольников разной формы. В их названии часто используют приставку «цирко», получая названия в стиле пентациркодекафлексагон. Расшифровать его можно так: кольцевой флексагон, у которого есть пять поверхностей, составленных из десяти многоугольников.

Куб Йошимото

Еще одна поделка-головоломка из бумаги – куб Йошимото – не является флексагоном, однако близка ему по духу. Его можно складывать, поворачивать, трансформировать, создавая новые фигурки, при этом куб не распадается на составные части:

Йошимото куб может показаться по-настоящему волшебным, ведь 8 небольших бумажных кубиков могут превращаться в змейку, звезду, кольцо, распадаться на две отдельные объемные звезды и снова трансформироваться. Но никакой магии здесь нет, сделать такой куб своими руками сможет даже начинающий, если проявит внимательность и будет следовать пошаговой инструкции.

Материалы:

• листы плотной бумаги;
• клей;
• острые ножницы или канцелярский нож;
• линейка;
• карандаш;
• скотч;
• шаблон развертки.

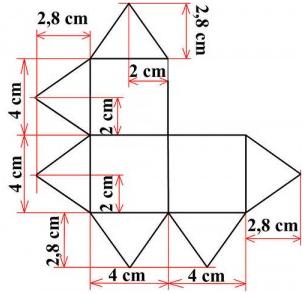
Описание: схему развертки можно распечатать или перерисовать с фото. Указанные размеры не являются неизменными, их можно пропорционально увеличивать, меняя размер готовой поделки. Очень важно оставлять полтора-два мм между элементами во время их соединения, это обеспечит лучшую подвижность куба.

Скреплять кубики лучше скотчем, хотя если вместо бумаги взять картон, придется воспользоваться клеем.

Пошагово весь процесс сборки куба показан в видео МК.

Видео: Учимся делать Йошимото куб

Йошимото куб удивительная, захватывающая головоломка, которая надолго завладеет вниманием взрослых и детей. Его легко сделать самому, с привлечением детей, ведь совместное творчество подарит массу положительных эмоций.

Методы складывания флексагонов

Возвращаясь к теме флексагонов, стоит упомянуть методы складывания, которые позволяют «обойти» все доступные поверхности пошагово. Было разработано несколько методов:

• v-flex. Используется для гексафлексагонов, от четырех поверхностей;
• tuckflex. Еще одно название – «лодка-гексаэрд», можно выполнить на гексафлексагонах с количеством плоскостей от четырех и больше;
• pinchflex. Используется для гексафлексагонов с количеством плоскостей от трех и больше.

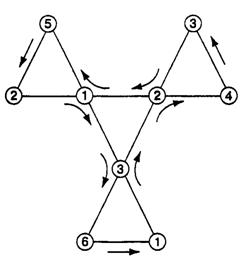
Последний метод больше известен под названием обход Таккермана. Он считается одним из самых простых вариантов, рассмотреть все доступные поверхности гексафлексагона. Согласно инструкции, необходимо взять флексагон за один уголок и раскрывая его до того момента, пока это возможно. Далее его поворачивают на шестьдесят градусов по ходу часовой стрелки, берут за соседний уголок и снова поэтапно раскрывают до конца:

При использовании обхода, грани раскрываются в определенном порядке: 1, 2, 5, 1, 2, 3, 4, 2, 3, 1, 6, 3 (или в обратном направлении). Этот порядок называется путь Таккермана.

Мастер — класс по складывания гексафлексагона

Сложить свой первый гексафлексагон из бумаги совсем не сложно, если следовать определенной схеме сборки. Делать это лучше всего опираясь на мастер-класс для начинающих. Он может быть как в формате видео, так и текстовом с пошаговыми фото.

Материалы:

• бумажная полоска 22*3,5 см (размеры можно пропорционально изменять);
• обычный клей;
• карандаш, разноцветные маркеры, линейка.

Техника сборки: на полосе размечают 10 равносторонних треугольников с чередованием вершин (вверх-вниз). Вершина первого из них смотрит вниз, тогда как последнего – вверх. Все грани треугольников должны быть одинаковыми – это залог правильной сборки флексагона. Разрезать ничего не нужно.

Грани можно заштриховать маркерами или пронумеровать от 1 до 10 с лицевой стороны, и от 11 до 20 с обратной. Одиннадцатый треугольник является оборотной стороной первого. Нумерацию можно сделать карандашом, тогда после сборки цифры легко сотрутся и не будут отвлекать от рисунка.

Когда треугольники размечены и подписаны, их сгибают по общим граням вперед-назад несколько раз.

Первые три треугольника загибают назад по общей грани 3 и 4 сегментов. После этого станут видны 11 и 12 треугольники.

Теперь последние четыре сегмента загибают вперед по линии соединения 6 и 7 треугольников.

После всех действий 11-ый треугольник скрыт под 19-ым. Его нужно аккуратно вывести наверх, поменяв их местами.

Последний шаг – загибание 20-го треугольника наверх, чтобы он закрыл 11-ый.

Гексафлексагон готов. Теперь можно экспериментировать с открытием поверхностей и наносить на них рисунки. Можно использовать готовые идеи раскрашивания или придумать свой уникальный узор – простор для фантазии просто безграничен!

Видео: Флексагон своими руками