Математика и оригами – точность и бумага

Математика и оригами имеют много общего. Оригами — это не простое умение складывать и сворачивать бумагу в разные фигуры. Оригами основано на математических законах геометрии и стереометрии и помогает развивать абстрактное мышление. Если развернуть любую фигуру оригами, то можно увидеть только множество симметричных линий. Чем сложнее фигура, тем больше линий и тем сложнее понять, как собрать с их помощью объёмный объект.

Математический раздел оригами не только наглядно решает геометрические задачи, но и помогает применять методы складывания в науке при выполнении сложных заданий, например, в космосе.

Статья предлагает познакомиться с оригами, помогающими наглядно понимать и решать математические задачи.

Наглядное решение уравнений

Правила Фудзиты — это семь основных правил, которые описывают посредством плоского оригами геометрическое построение. Презентация геометрических правил с помощью сложения оригами поможет наглядно понять школьникам решение линейных, квадратных, кубических уравнений.

Основная суть всех математических правил: возможность выполнения бумажной складки с помощью соединения уже построенных элементов — линий и точек. При этом фигура всегда остаётся плоской.

Семь правил:

1. Через любые точки p1 и p2 возможно перегнуть лист так, чтобы они оказались на складке.
2. Бумагу возможно сложить таким образом, чтобы точка p1 совместилась с точкой p2.
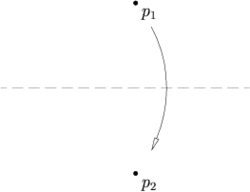
3. Лист с построенными на нём прямыми l1 и l2 можно согнуть так, что l1 перейдёт в l2.
4. Лист с прямой l1 и точкой p1 можно согнуть так, что p1 окажется на перегибе, а l1 — перпендикулярно ему.
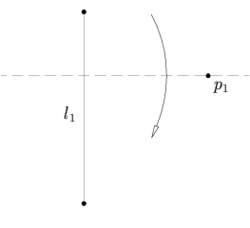
5. Бумагу с точками p1 и p2 и прямой l1 можно перегнуть так, что p1 окажется на перегибе, а p2 — на l1.
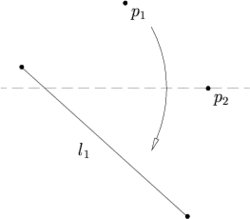
6. Лист с построенными точками p1 и p2 и прямыми l1 и l2 можно согнуть таким образом, что p1 окажется на l1, а p2 — на l2.
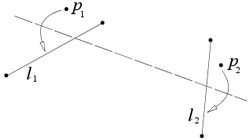
7. Бумагу с заданными на ней прямыми l1 и l2 и точкой p возможно перегнуть так, что l2 передастся самой себе и станет перпендикулярной перегибу, а p ляжет на l1.

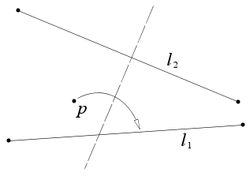
Математические правило № 6 или правило Маргериты Пьяцоллы: Белок объединяет все остальные правила. Можно сказать, что правила 1-5 и 7 — более подробное объяснение правила № 6.

Полностью все правила описал Жак Жюстин и одновременно с ним были сформулированы правила 1-6 японским математиком Фумиаки Фудзитой. Математическое правило 7 добавил позднее Косиро Хатори.

Правила можно расширить за счёт возможности делать на бумаге несколько перегибов. Однако на практике это может оказаться сложнее, чем в теории.

Экономичное сложение

Миура-ори – паттерн (чертёж) жёсткого оригами, позволяющий разворачивать и сворачивать большие поверхности одним движением руки.

Впервые паттерн был разработан Корё Миурой — японским физиком — в 1970 году для разворачивания в открытом космосе спутниковых солнечных батарей. Также этот принцип используют для сворачивания карт или чертежей большого формата.

Конечно, сворачивать бумагу в несколько слоёв умеет любой человек, но метод Миуры позволяет быстро развернуть даже большие форматы при любых условиях, например, при ветре или в космосе, а кроме того, из-за отсутствия многослойных сгибов снимает нагрузку на бумагу.

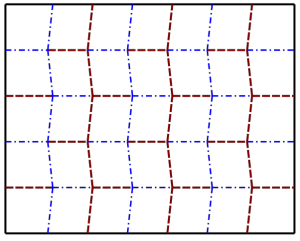
Лист бумаги, сложенный методом Миура-ори, в развёрнутом виде имеет вертикальные ряды косых линий сгибов. Горизонтальные линии при этом прямые. При развороте фигуры Миура-ори схема может показаться довольно простой, выглядит она так:

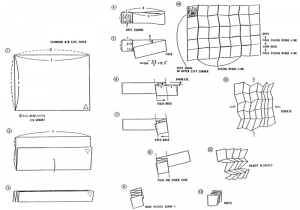
Однако на практике возникает вопрос: как свернуть лист так, чтобы на нём получились аккуратные и равные по ширине и длине косые вертикальные перегибы? Начинается сборка с простой гармошки: бумагу необходимо поочерёдно перегибать в одну и в другую стороны на одинаковую ширину. Получились горизонтальные прямые перегибы. Затем края получившейся полоски перегибают также гармошкой, но под углом.

Видео-уроки математического оригами

Наглядно изучить способы сложения оригами методом Миуры и посмотреть презентацию действия оригами рекомендуется по видеороликам ниже:

Этот метод используют не только учёные, но и дизайнеры при создании необычного декора, например, стен, штор или светильников.

О рубле, гребёнке и периметре

Задача о мятом рубле или задача о салфетке Маргулиса открывает список математических задач В.И. Арнольда.

Суть задачи сводится к вопросу: можно ли увеличить периметр прямоугольного листа бумаги (на примере бумажного рубля) с помощью сложения прямоугольника в фигуру? При этом есть условие, что нельзя рвать или резать бумагу.

Задача была сформулирована и опубликована в 1956 году математиком В.И. Арнольдом. Позднее в США задача прославилась как «салфетка Маргулиса» (по имени советского математика, эмигрировавшего в США).

Отчасти решили проблему физик Роберт Лэнг и математик Иван Ященко. Полностью задачу разрешил Алексей Тарасов. Решение получило название «расчёска Тарасова».

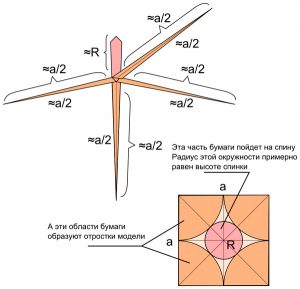
Для того чтобы понять основной секрет решения задачи (как увеличить периметр за счёт сложения), необходимо провести стереометрический эксперимент. Для этого необходимо сделать следующее:

1. Квадратный лист разбить на равные клетки и раскрасить их в шахматном порядке двумя цветами (например, синим и красным).
2. Прочертить в каждой клетке из центра 16 лучей.
3. Нарисовать в центре каждой клетки определённого цвета (например, красного) зелёные звёздочки.
4. Перегнуть бумагу по диагоналям и сделать из него прямоугольник, а затем треугольник (в одной половине получаются синие слои, а в другой — красные).
5. Начать сминать фигуру так, чтобы синие и красные слои стали выпуклыми и смотрели наружу.

В результате должна получиться фигура, напоминающая гребёнку или расчёску. С одной стороны собраны вместе красные и синие слои, а с другой находятся зелёные лучи по количеству красных клеток.

Общий математический алгоритм сборки расчёски Тарасова можно посмотреть по видеоролику:

Визуально периметр уменьшился, но если увеличивать количество лучей в каждой клетке или количество клеток, то периметр фигуры можно увеличивать до бесконечности и в результате он сможет стать больше изначальной фигуры.